민주시민교육, 법교육 연구

교육연구와 통계방법(5) -정규분포, 표집분포

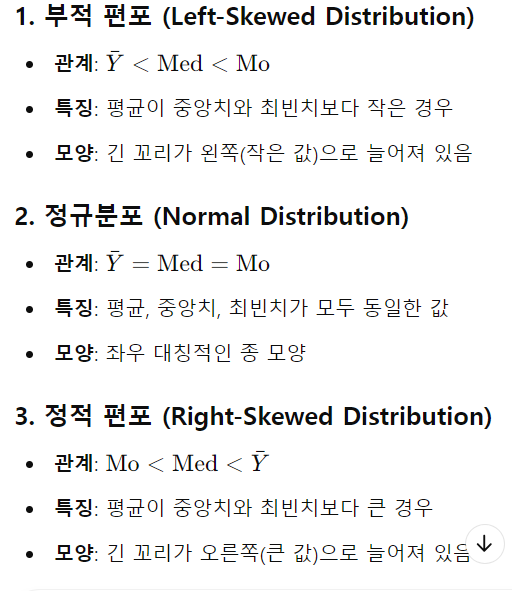
1. 정규분포□ 정규분포(normal distribution)가 왜 중요한가?실제 많은 양적 변수가 대략적으로나마 정규분포를 이루고 있어서종속변수가 양적 변수일 경우, 대부분의 추리통계에서 이 변수가 모집단에서 정규분포를 이룰 것으로 가정어떤 분포가 적어도 대략적으로라도 정규분포를 이룬다고 가정할 수 있다면, 이에 대한 다양한 추론이 가능주어진 모집단에서 무한히 많은 수의 표본을 추출했을 때, 이 표본 평균들의 분포는 이론적으로 정규분포 1. 정규분포□ 정규분포(normal distribution)란?양적 변수, 연속변수가 이루는 분포이론 정립: Laplace, Gauss, Galton좌우대칭의 종을 엎어놓은 모양 (bell-shaped)의 분포▣ 평균 = 중앙치 = 최빈치 ▣ 단봉분포 (unimodal..

교육연구와 통계방법(4) -분산도

변수의 분산분포의 형태와 중심경향치부적편포 (negatively Skewed ) 꼬리가 가늘게 음으로 늘어져, 정적편포(postively skewed)꼬리가 가늘게 음으로 늘어져.왜도 : Skewness  분포의 비대칭 정도, 분포가 기울어진 방향과 정도를 나타낸다.왜도 0 = 정규분포, 왜도 음수이면 부적편포, 양수이면 정적편포📊 변산(variability) 혹은 분산도(variation)점수분포가 얼마나 퍼져 있는지, 즉 다양성의 정도관련 개념: 범위, 사분위간 범위, 분산, 표준편차📏 범위 (range)범위 = 최고치 - 최저치(연속성을 가정하는 경우) 범위 = 최고치 - 최저치 + 측정 단위📦 사분위간 범위 (interquartile range)백분위 75와 백분위 25 사이의 거리 Q3−Q..

교육연구와 통계방법(3) - 중심경향값

중심경향 (central tendency) 이란?모집단 또는 표본으로부터 얻은 자료를 그래프로 그려보면, 대부분 많은 자료들이 특정한 값으로 몰리는 현상을 보임. 중심경향치란?중심경향을 나타내는 특정한 값으로, 분포의 중심에서 자료를 대표하는 값  유사 개념 - 조화평균, 기하평균, 가중평균 등조화평균: n개의 양수에 대해 그 역수들을 산술평균한 것의 역수. 여러 집단의 사례수가 다른 경우, 이를 조정하기 위해 주로 사용기하평균: n개의 양수가 있을 때, 이들 수의 곱의 n제곱근의 값가중평균: 가중치를 적용하여 구한 산술평균  평균 또는 산술평균 (arithmetic mean)장점평균은 가감승제 적용이 용이모집단 평균의 추정치로서 사용되는데 바람직한 특성 보유 (특히 표본이 변해도 평균은 다른 중심경향치..

막대그래프▪ 질적 변수에 가장 적합▪ ‘무응답’이나 ‘기타’ 항목에 대한 처리는 신중을 기해야▪ 분류항목의 개수에 따라 세로 막대그래프와 가로 막대 그래프 선택 가능▪ 분류항목의 제시순서는 연구자가 임의로 결정 가능▪ 분류항목 내에서 동일 내용을 다시 하위집단 별로 비교하고자 할 때에도 사용 가능-막대의 넓이를 같게, 막대와 막대사이의 공간 같게 그려야 함.막대그래프 데이터SPSS 21 실제 선그래프▪ 양적 변수에 대해 사용, 비연속변수(특정수치만 가짐)▪ 시간의 흐름에 따른 추이를 나타낼 때 유용▪ X축과 Y축 모두 양적 변수이므로, X축과 Y축의 최소값, 최대값의 크기 선정과 눈금간 간격 유지에 유의해야▪ 유사한 내용의 그래프를 반복해서 제시하는 경우, X축과 Y축의 간격이 유사하게 유지되어야-현대 ..

두자리 수 난수표 이용하여 1~200개 단순무선표집으로 추출하기 해결 방법: 1~200을 균등하게 뽑는 방법🔹 방법 1: 두 자리 난수를 두 번 뽑아 1~200으로 변환난수표에서 두 자리 숫자(00~99)를 하나 뽑습니다.이 숫자가 1~100이면 그대로 사용, 0이면 100번으로 사용이미 뽑은 숫자에 100을 더한 값도 표본에 포함이 과정을 중복되지 않게 반복하여 10명을 뽑음✅ 예시난수표에서: 07, 45, 88, 23, 56, 91, 12, 99, 04, 67 을 뽑았다면1차 그룹: 7, 45, 88, 23, 56, 91, 12, 99, 4, 672차 그룹: 107, 145, 188, 123, 156, 191, 112, 199, 104, 1671차 그룹과 2차 그룹을 섞어서 최종 10명 선정🔹 장..

□ 모수치와 추정치✅ 모수치(parameter)모집단이 지니고 있는 속성. 평균은 μy(뮤), 표준편차는 σy(시그마)로 표기 (그리스/로마 알파벳 사용)✅ 통계치(statistic)표본이 지니고 있는 속성. 평균은 Ȳ(와이바), 표준편차는 sy(에스와이)로 표기✅ 추정치(estimates)직접 구할 수 없는 모집단의 모수치를 표본의 속성을 토대로 추정한 값. 평균은 μ ̂(뮤헷), 표준편차는 σ ̂(시그마헷)로 표기 매개변수 : 독립변수가 직접 종속변수에 영향을 미치는 것이 아니라 어떤 변수를 통해 간접적으로 영향을 미칠때 중간에 독립변수의 영향을 종속변수에 매개해주는 변수. 종속변수에 영향을 주는 독립변수 이외의 변수로서 연구에서 통제되어야 할 변수.조절변수 : 두 변수 간의 관계가 제3의 변수의 수..

이훈영(2015). 이훈영교수의 연구조사방법론 제 2판, 청람출판사, pp, 694-757 로지스틱 회귀분석 : 분석하고자 하는 대상들이 두 집단 혹은 그 이상의 집단으로 나누어진 경우에는 개별 관측지들이 어느 집단으로 분류될 수 있는가를 분석하고 이를 예측하는 모형을 개발하는데 사용되는 대표적인 통계기법. 종속변수가 명목척도로 측정된 범주형 질적변수인 경우에 사용함.  이항로지스틱 회귀분석 : 비선형함수모형, 개별 관측지가 2개 집단 중에 어느 집단에 속하는게 나타내는 이항 범주형 종속변수 예측. 종속변수 값으로 범주값을 직접 사용하지 않고 종속변수가 특정한 범주값, 예를 들어 1의 값을 가질 확률을 종속변수값으로 사용. 확률값의 오즈를 종속변수로 하는 2차적인 치환. p/1-p. 자연로그로 변환.  ..

이훈영(2015). 이훈영교수의 연구조사방법론 제 2판, 청람출판사, pp, 427-444 다중회귀분석 : 2개이상의 독립변수와 종속변수 간의 관계를 설명하고 종속변수 값의 예측에 사용할 수 있는 회귀식 도출하는 분석방법.    유용한 독립변수를 선정하기 위해 어느 변수의 설명력이 높은지 선별하는 방법 : 전진선택방식(여러 개의 독립변수들 중에서 가장 중요한 변수의 순으로 하나씩 선택, F값 확인), 후진제거방식(불필요한 변수 제거, F값, 유의성 확인), 단계선택방식(변수 선택 동시에 변수들 중 다중공선성 변수 제거), 제거(특정변수 제거)더미변수를 이용한 회귀분석 : 명목척도를 이항변수로 바꾸어 회귀분석함.  비선형회귀분석 : 독립변수를 변환하여 종속변수와 선형관계가 되도록 조정. 때에따라서 종속변수..

이훈영(2015). 이훈영교수의 연구조사방법론 제 2판, 청람출판사, pp, 400-427 회귀 : 한바퀴 돌아서 다시 제자리로 옴. 평균으로 되돌아간다는 의미.회귀선 : 주어진 x값의 각 점에 대응하는 Y값들의 평균을 관통하는 직선회귀분석 : 독립변수x값이 주어졌을때 대응하는 종속변수y값을 예측하거나 종속변수에 대한 독립변수의 영향을 설명하는데 사용되는 분석방법. 다중공선성 고려(독립변수들 간의 상관관계). 공차한계를 이용하여 다중공선성 확인. 1-R², 분산확대지수(VIF=1/공차한계) 단순회귀분석 : 독립변수가 하나일 경우에 종속변수의 관계를 분석하여 독립변수가 종속변수에 미치는 영향을 분석하는 방법.  최소자승법 : 회귀선과 관측치들간의 차이를 제곱하여 모두 더한값. 잔차의 제곱합이 최소가 되도록..

이훈영(2015). 이훈영교수의 연구조사방법론 제 2판, 청람출판사, pp, 359-395 분산분석은 3개이상 집단간의 평균이 서로 다른지 검정하는 분석방법. 집단간의 평균들이 다르고, 집단내 관측치가 그 집단의 평균으로부터 퍼져있는 분산, 집단 내 평균제곱에 비해 집단간 평균제곱의 크기가 상대적으로 크면 집단의 평균들이 넓게 퍼져 서로 명확하게 다르다고 판단.  단일변량분석은 단일 종속변수의 평균값이 집단 간의 차이가 있는지 분석. 다변량분산분석은 2개 이상 종속변수들의 평균값들, 평균벡터의 집단간 차이를 동시에 비교, 분석하는 방법이다. 단일변량분석에서 독립변수의 수에 따라 일원분석분석(단일 독립), 이원분산분석(2개 독립변인)으로 나눔.  일원분산분석표    이원분산분석 : 주효과, 상호작용효과 고..