민주시민교육, 법교육 연구

교육연구과 통계검증(11)- 중다회귀분석

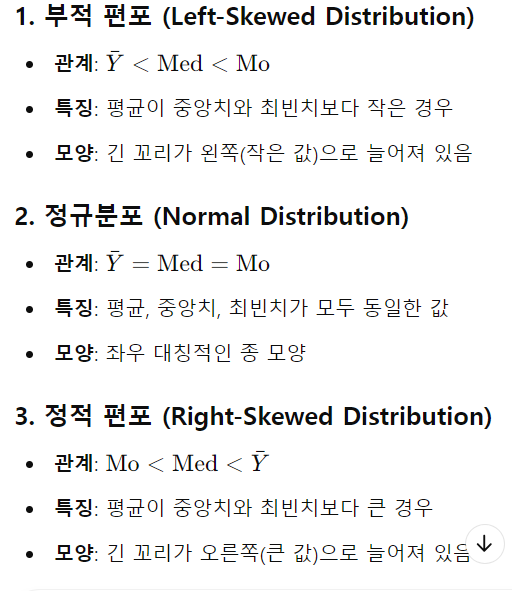
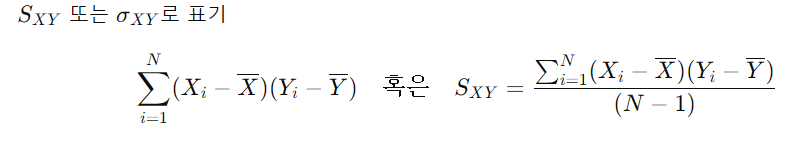□ 중다회귀분석이란?여러 개의 독립변수를 사용하여 한 개의 양적 변수인 종속변수를 설명, 예측하기 위한 통계모형 □ 중다회귀분석의 목적:여러 개의 특정 독립변수들이 종속변수에 대하여 가지는 효과를 파악하되,다른 독립변수들(공변인; covariates)에 의한 영향/오염을 통제하고 순수한 효과를 파악하기 위해 실시종속변수를 가장 잘 예측하는, 또는 가장 많이 설명하는 독립변수가 어떤 것인지 파악하기 위해 실시주의: 회귀분석의 결과를 토대로 "인과관계 추론"은 부적절 □ 중다회귀계수의 추정최소제곱법 (ordinary least square estimation) 중다회귀분석의 기본 가정상관분석과 유사선형성다변량 정규성(multivariate normality) 등분산성 □ Outlier(이상치) 확인◼ Dis..

교육연구과 통계검증(10)- 회귀

1. 단순회귀분석의 기본개념□ 상관분석과 회귀분석의 차이■ 연구의 목적:상관분석은 두 변수간 관련성의 크기를 분석회귀분석은 독립변수를 이용해서 종속변수를 예측, 설명하고자 하는 경우에 사용⇒ 회귀분석의 경우 “방향성” 존재□ 회귀분석 (regression analysis)독립변수를 사용해서 종속변수를 설명, 예측하고자 하는 경우에 사용독립변수의 수에 따라서 단순회귀분석, 중다회귀분석 □ 왜 회귀분석(regression)이라고 하는가?Regression toward the mean단순회귀분석의 경우, 표준점수로 변환된 종속변수는 역시“표준점수로 변환된 독립변수와 두 변수간 상관계수의 곱”으로 예측대부분의 경우 X와 Y의 상관은 1.0보다 작은 값이므로, Y값은 X보다 더 평균에서 가까운 값으로 예측예시:X..

교육연구과 통계검증(9)- 상관

공분산과 상관계수변수간 관련성이란?두변수간 서로 관련성이 있는지? 즉 한 변수가 변해감에 따라 다른 변수가 함께 변해가는가?상관관계와 인과관계엄밀하게 통제된 실험설계에서는 상관관계를 인과관계로 해석 가능하지만 조사연구에서는 상관관계를 인과관계 보다는 변수간 '상호관련성'으로 해석해야함 1-1. 공분산▣ 공분산두 변수가 동시에 변하는 정도로, 한 변수가 얼마만큼 변할 때 다른 변수는 얼마만큼 변해가는 지의 정도를 X와 Y의 평균 (𝑋̄, 𝑌̄)을 기준으로 계산X 변수의 편차와 Y 변수의 편차를 구하여 곱한 값들의 평균. ▣ 공분산의 특징■ 지역독립성 (location-free) → 충족□ 두 변수에 일정한 값을 규칙적으로 더하거나 빼도 동일 수치□ 평균도 함께 변하기 때문■ 척도독립성 (scale-fr..

1. 평균에 대한 표집분포 : Z분포와 t분포□ 평균에 대한 표집분포모집단의 분산을 알고 있는 경우, 정규분포로 분포모집단의 분산을 모르는 경우,□ t분포■ W. Gosset (1908)(정규분포에서 표본을 추출하여 표집분포를 구하되)모집단의 표준편차를 알지 못하여, 표본의 표준편차로 모집단의 표준편차를 추정하여 사용하는 경우,■ 표본의 크기(N) 혹은 자유도(df = N-1) 가 작을수록 T 분포의 특징-평균이 '0'인 좌우대칭 분포-표준편차가 표준정규분포보다 큰 분포자유도가 무한대이면 표준정규분포와 거의 동일자유도가 30이상이면 표준 정규분포에 근사 ◼ z검증과 t검증▪ 모집단의 분산을 알고 있는지 여부에 따라 결정▫ 모집단의 분산을 알고 있는 경우 ⇒ z검증▫ 모집단의 분산을 모르기 때문에 표본 분..

불편파 추정치와 자유도좋은 추정치란?-불편파성(unbiasedness)추정치의 기대값이 모수치와 동일한 경우기대값이란? 발생확률을 가중치로 한 가중평균-효율성(effectiveness)표준오차가 최대한 작아야-일관성(consistency)표본의 크기가 커질수록 표준오차가 작아지는 경향  자유도 (degree of freedom; df, ν)통계적 추정을 할 때 표본자료 중 모집단에 대한 정보를 주는 독립적인 자료의 수 표본 평균의 자유도는→ n표본 분산의 자유도는→ (n - 1) 편차의 합이 ‘0’을 충족시키고, 즉 평균을 유지하면서 자유롭게 어떤 값을 가질 수 있는 사례 수모집단의 평균을 알지 못하여 표본평균을 사용하여 분산을 구해야 하기 때문에, 표본분산은 표본평균의 값에 의하여 제한을 받으므로 2...

3. 가설검증의 기본 개념■ 영가설과 대립가설영가설(𝐻₀), 귀무가설일반적으로 연구자가 연구에서 부정하고자 하는 내용이 담긴 가설.  대립가설(𝐻ₐ 또는 𝐻₁)일반적으로 연구자가 연구에서 주장하고자 하는 내용이 담긴 가설영가설이 부정되었을 때 TRUE로 남는 잠정적 진술영가설을 사용하는 이유특정 사실이 TRUE라는 걸 증명하기보다는 FALSE라는 것을 증명하기가 더 쉬움→ 가설검증의 출발점 제공 ->  1종오류를 극소화해야 바람직한 연구임. 📊 가설검정의 오류 개념 시각화 설명이 그래프는 **가설검정(hypothesis testing)**에서의 두 가지 주요 오류인 **제1종 오류(α)**와 **제2종 오류(β)**를 시각적으로 설명한 것입니다. 두 개의 종 모양 곡선(정규분포곡선)이 서로 겹쳐 ..

1. 정규분포□ 정규분포(normal distribution)가 왜 중요한가?실제 많은 양적 변수가 대략적으로나마 정규분포를 이루고 있어서종속변수가 양적 변수일 경우, 대부분의 추리통계에서 이 변수가 모집단에서 정규분포를 이룰 것으로 가정어떤 분포가 적어도 대략적으로라도 정규분포를 이룬다고 가정할 수 있다면, 이에 대한 다양한 추론이 가능주어진 모집단에서 무한히 많은 수의 표본을 추출했을 때, 이 표본 평균들의 분포는 이론적으로 정규분포 1. 정규분포□ 정규분포(normal distribution)란?양적 변수, 연속변수가 이루는 분포이론 정립: Laplace, Gauss, Galton좌우대칭의 종을 엎어놓은 모양 (bell-shaped)의 분포▣ 평균 = 중앙치 = 최빈치 ▣ 단봉분포 (unimodal..

변수의 분산분포의 형태와 중심경향치부적편포 (negatively Skewed ) 꼬리가 가늘게 음으로 늘어져, 정적편포(postively skewed)꼬리가 가늘게 음으로 늘어져.왜도 : Skewness  분포의 비대칭 정도, 분포가 기울어진 방향과 정도를 나타낸다.왜도 0 = 정규분포, 왜도 음수이면 부적편포, 양수이면 정적편포📊 변산(variability) 혹은 분산도(variation)점수분포가 얼마나 퍼져 있는지, 즉 다양성의 정도관련 개념: 범위, 사분위간 범위, 분산, 표준편차📏 범위 (range)범위 = 최고치 - 최저치(연속성을 가정하는 경우) 범위 = 최고치 - 최저치 + 측정 단위📦 사분위간 범위 (interquartile range)백분위 75와 백분위 25 사이의 거리 Q3−Q..

중심경향 (central tendency) 이란?모집단 또는 표본으로부터 얻은 자료를 그래프로 그려보면, 대부분 많은 자료들이 특정한 값으로 몰리는 현상을 보임. 중심경향치란?중심경향을 나타내는 특정한 값으로, 분포의 중심에서 자료를 대표하는 값  유사 개념 - 조화평균, 기하평균, 가중평균 등조화평균: n개의 양수에 대해 그 역수들을 산술평균한 것의 역수. 여러 집단의 사례수가 다른 경우, 이를 조정하기 위해 주로 사용기하평균: n개의 양수가 있을 때, 이들 수의 곱의 n제곱근의 값가중평균: 가중치를 적용하여 구한 산술평균  평균 또는 산술평균 (arithmetic mean)장점평균은 가감승제 적용이 용이모집단 평균의 추정치로서 사용되는데 바람직한 특성 보유 (특히 표본이 변해도 평균은 다른 중심경향치..

막대그래프▪ 질적 변수에 가장 적합▪ ‘무응답’이나 ‘기타’ 항목에 대한 처리는 신중을 기해야▪ 분류항목의 개수에 따라 세로 막대그래프와 가로 막대 그래프 선택 가능▪ 분류항목의 제시순서는 연구자가 임의로 결정 가능▪ 분류항목 내에서 동일 내용을 다시 하위집단 별로 비교하고자 할 때에도 사용 가능-막대의 넓이를 같게, 막대와 막대사이의 공간 같게 그려야 함.막대그래프 데이터SPSS 21 실제 선그래프▪ 양적 변수에 대해 사용, 비연속변수(특정수치만 가짐)▪ 시간의 흐름에 따른 추이를 나타낼 때 유용▪ X축과 Y축 모두 양적 변수이므로, X축과 Y축의 최소값, 최대값의 크기 선정과 눈금간 간격 유지에 유의해야▪ 유사한 내용의 그래프를 반복해서 제시하는 경우, X축과 Y축의 간격이 유사하게 유지되어야-현대 ..