변수의 분산
분포의 형태와 중심경향치
부적편포 (negatively Skewed ) 꼬리가 가늘게 음으로 늘어져, 정적편포(postively skewed)꼬리가 가늘게 음으로 늘어져.

왜도 : Skewness 분포의 비대칭 정도, 분포가 기울어진 방향과 정도를 나타낸다.
왜도 0 = 정규분포, 왜도 음수이면 부적편포, 양수이면 정적편포


📊 변산(variability) 혹은 분산도(variation)
- 점수분포가 얼마나 퍼져 있는지, 즉 다양성의 정도
- 관련 개념: 범위, 사분위간 범위, 분산, 표준편차
📏 범위 (range)
- 범위 = 최고치 - 최저치
- (연속성을 가정하는 경우) 범위 = 최고치 - 최저치 + 측정 단위
📦 사분위간 범위 (interquartile range)
- 백분위 75와 백분위 25 사이의 거리 Q3−Q1
- 박스 플롯에서 사용된 박스의 높이


예시로 2, 3, 5, 2의 데이터를 분산, 표준편차를 나타내면 (분산 사례수 n 로 나누지 않고 n-1로 나눔)

기술통계량
N 최소값 최대값 평균 표준편차 분산
VAR00001 4 2.00 5.00 3.0000 1.41421 2.000
유효수 (목록별) 4
-분산이 크면 이질적이고 분포의 높이, 봉이 낮다고 하고
분산이 작으면 분포의 봉이 높다. 뽀족한 정도, 분포의 봉을 첨도라고 함.
정규분포의 첨도는 0이며, 첨도가 0보다 작으면 정규분포보다 낮은 평성, 0보다 크면 정규분포보다 더 뽀족한 급첨이라고 함.
기말점수, 2,3,5,2 데이터의 z점수 변환 SPSS
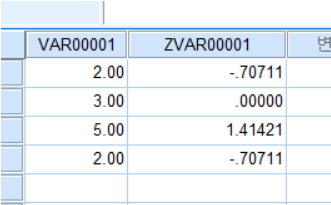
4. 데이터의 변환과 기술통계
📌 데이터의 변환과 분포의 형태
✅ 데이터를 선형 변환하는 경우
- 선형변환: y′=ay+b
- 평균과 표준편차만 변화할 뿐, 분포의 형태는 그대로 유지
✅ 분포의 형태를 변화시키고자 하는 경우
- 비선형변환을 실시하면, 평균, 표준편차 이외에 분포의 형태도 함께 변화
- 비선형변환 예시:
- Log 변환 (자연로그 -> 정규분포)
- 백분위를 사용하여 원래의 점수를 백분위 점수로 변환하는 normalizing (정규화)

서울대학교 교육통계 강의 자료. 사범대학교 교육학과 박현정교수
성태제(2019). 현대기초통계학 이해와 적용 제 8판. 학지사. pp, 95-120
'교육연구방법' 카테고리의 다른 글
| 교육연구과 통계검증(8)- t검증 (0) | 2025.04.09 |
|---|---|
| 교육연구와 통계방법(7) - 가설검증의 관점(불편파성, 구간추정, 표본크기) (0) | 2025.04.08 |
| 교육연구와 통계방법(6)- 가설검증 (0) | 2025.04.08 |
| 교육연구와 통계방법(5) -정규분포, 표집분포 (0) | 2025.04.07 |
| 교육연구와 통계방법(3) - 중심경향값 (0) | 2025.04.06 |
| 교육연구와 통계방법(2)- 그래프 (0) | 2025.04.03 |
| 두자리 수 난수표 이용하여 1~200개 단순무선표집으로 추출하기 (0) | 2025.04.02 |
| 교육연구와 통계방법(1) - 모수치, 추정치, 매개변수, 조절변수, 혼재변수 (0) | 2025.04.01 |