반응형
1. 정규분포
□ 정규분포(normal distribution)가 왜 중요한가?
- 실제 많은 양적 변수가 대략적으로나마 정규분포를 이루고 있어서
- 종속변수가 양적 변수일 경우, 대부분의 추리통계에서 이 변수가 모집단에서 정규분포를 이룰 것으로 가정
- 어떤 분포가 적어도 대략적으로라도 정규분포를 이룬다고 가정할 수 있다면, 이에 대한 다양한 추론이 가능
- 주어진 모집단에서 무한히 많은 수의 표본을 추출했을 때, 이 표본 평균들의 분포는 이론적으로 정규분포
1. 정규분포
□ 정규분포(normal distribution)란?
- 양적 변수, 연속변수가 이루는 분포
- 이론 정립: Laplace, Gauss, Galton
- 좌우대칭의 종을 엎어놓은 모양 (bell-shaped)의 분포
▣ 평균 = 중앙치 = 최빈치 ▣ 단봉분포 (unimodal dist.) - 면적 = 1
- 정규분포의 특징은 평균과 표준편차로 규정 가능.
Y∼N(μ,σ2)

□ 표준정규분포
- 평균이 '0'이고 표준편차가 '1'인 정규분포 (z분포)
- 따라서 다음 관계가 성립
-
- □ -1 < z < +1 사이에 68.26%
- □ -2 < z < +2 사이에 95.44%
- □ -3 < z < +3 사이에 99.72%

2. 표집분포와 가설검증
□ 표집분포
- 주어진 모집단에서 동일한 크기의 표본을 무한반복 추출한다고 가정했을 때, 이 표본들에서 구한 통계치들이 이루는 분포
- 실제 존재하는 분포가 아닌 가상적/이론적 분포
■ 평균의 표집분포
- 주어진 모집단에서 무한히 많은 수의 표본을 추출해서 구한 표본 평균
2. 표집분포와 가설검증
□ 평균의 표집분포
- 분포의 모양: 정규분포 (n > 30인 경우)
- 분포의 평균: 모집단의 평균
- 분포의 표준편차:
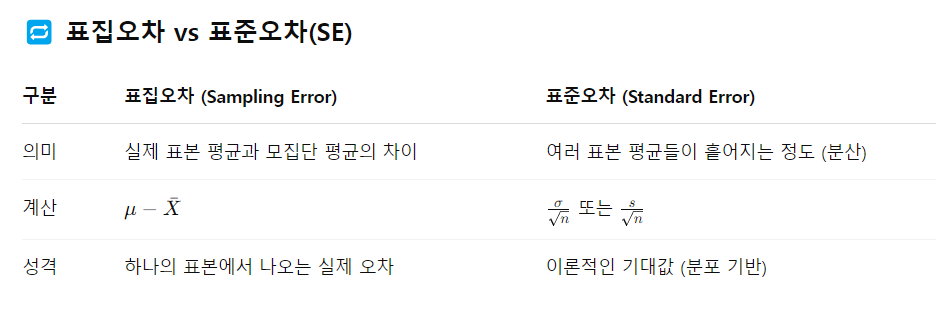
▣ 표준오차 (standard error) : 표집분포의 표준편차 
▣ 모집단의 표준편차를 표본크기의 제곱근으로 나누어준 값
▣ Cf. 표집오차 (sampling error)
■ 가설검증에서의 표집분포의 역할
- 모집단에 대한 가설을 검증하고자 할 때
표집분포에 근거하여 기각역과 채택역을 설정하고, - 표본에서 구한 통계치가 어디에 위치하는지를 토대로 가설 채택 여부 결정

- 기대값 : 변수의 기대값은 모집단의 평균이 될 수 있음.

전이법칙 : 어떤 변수에 상수를 더하면 평균에 더한 만큼 상수를 더하면 되고, 분산은 변함없음.
척도법칙 : 변수에 일정 상수를 곱하거나 나누었을때는 그대로 곱하거나 나누면 평균이 되지만, 분산은 상수 값의 제곱곱하거나 나눈값과 같다.
중심극한정리 : 표집분포의 평균은 모집단의 평균이고, 표집분포의 분산은 모집단의 분산을 표본의 크기로 나눈 것 과 같으며, 표본의 크기가 충분히 클때(n>30) 모집단의 분포와 상관없이 정규분포가 됨을 말함.
서울대학교 교육통계 강의 자료. 사범대학교 교육학과 박현정교수
성태제(2019). 현대기초통계학 이해와 적용 제 8판. 학지사. pp, 219-245
반응형
'교육연구방법' 카테고리의 다른 글
| 교육연구과 통계검증(9)- 상관 (0) | 2025.04.11 |
|---|---|
| 교육연구과 통계검증(8)- t검증 (0) | 2025.04.09 |
| 교육연구와 통계방법(7) - 가설검증의 관점(불편파성, 구간추정, 표본크기) (0) | 2025.04.08 |
| 교육연구와 통계방법(6)- 가설검증 (0) | 2025.04.08 |
| 교육연구와 통계방법(4) -분산도 (0) | 2025.04.06 |
| 교육연구와 통계방법(3) - 중심경향값 (0) | 2025.04.06 |
| 교육연구와 통계방법(2)- 그래프 (0) | 2025.04.03 |
| 두자리 수 난수표 이용하여 1~200개 단순무선표집으로 추출하기 (0) | 2025.04.02 |