반응형
3. 가설검증의 기본 개념
■ 영가설과 대립가설
- 영가설(𝐻₀), 귀무가설
일반적으로 연구자가 연구에서 부정하고자 하는 내용이 담긴 가설. - 대립가설(𝐻ₐ 또는 𝐻₁)
일반적으로 연구자가 연구에서 주장하고자 하는 내용이 담긴 가설
영가설이 부정되었을 때 TRUE로 남는 잠정적 진술 - 영가설을 사용하는 이유
특정 사실이 TRUE라는 걸 증명하기보다는 FALSE라는 것을 증명하기가 더 쉬움
→ 가설검증의 출발점 제공

-> 1종오류를 극소화해야 바람직한 연구임.
📊 가설검정의 오류 개념 시각화 설명
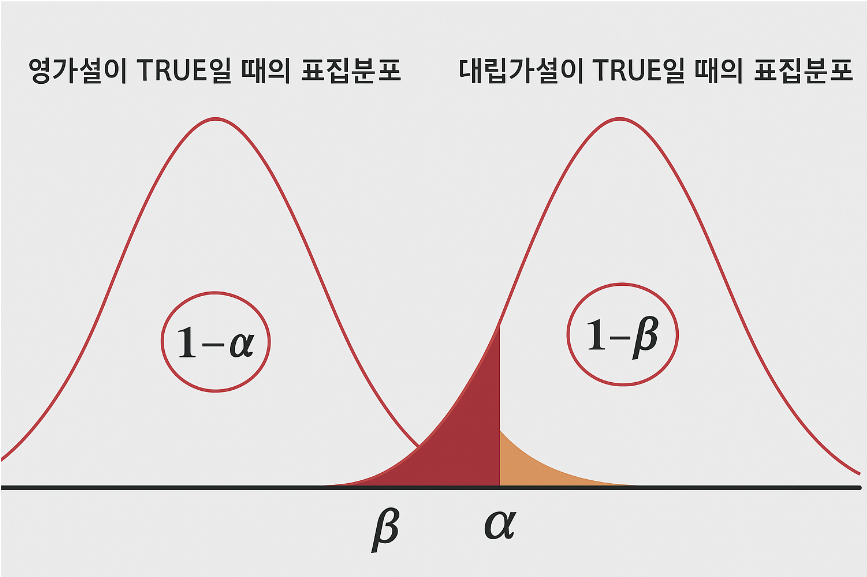
이 그래프는 **가설검정(hypothesis testing)**에서의 두 가지 주요 오류인 **제1종 오류(α)**와 **제2종 오류(β)**를 시각적으로 설명한 것입니다. 두 개의 종 모양 곡선(정규분포곡선)이 서로 겹쳐 있으며, 각각은 다음을 나타냅니다:
✅ 곡선 설명
- 왼쪽 곡선: “영가설이 TRUE일 때의 표집분포”
- 오른쪽 곡선: “대립가설이 TRUE일 때의 표집분포”
❗ 오류의 의미
- 🔶 제1종 오류 (α):
- 🔴 제2종 오류 (β):
📈 검정력 (1−β)
- 대립가설이 참일 때, 우리가 영가설을 정확히 기각할 수 있는 확률
- 그림에서 오른쪽 곡선 아래 β를 제외한 나머지 영역입니다.
- 이 값이 클수록 좋은 검정(test)입니다.
🔄 1−α (신뢰도)
- 영가설이 참일 때, 올바르게 수용할 확률
- 그림에서 왼쪽 곡선에서 α를 제외한 나머지 넓은 영역입니다.

유의수준 (level of significance), 1종오류.
- 가설검증에서 영가설이 TRUE일 때 이 영가설이 잘못되었다고 오판하는, 즉 실수할 확률을 어느 정도까지 감수할 것인지를 미리 결정하는 것
- 이렇게 연구에 있어서 심각한 오판을 내릴 확률, 즉 제1종의 오류의 최대허용수준
- α로 표기하며, 일반적으로 α = 0.05, 0.01, 0.001로 설정
- 각 연구에서 유의수준의 결정은 연구자의 이론적 배경, 경험적 배경(특히 표본 크기 등), 연구에서 오판의 심각성 등에 의해서 결정
● 등가설과 부등가설
- 등가설: 영가설과 대립가설에 유효한 차이는 가설(차이가 있다/없다) → 가설 검증은 양방 검증 (two-tailed test) 통해 실시
- 부등가설: 영가설과 대립가설에 부등호가 있는 가설 (더 크다/크지 않다 혹은 작다/작지 않다)로, 두 쪽은 항상 영가설에 존재
→ 가설 검증은 일방 검증 (one-tailed test) 통해 실시 - 영가설 (H₀): μ_pre = μ_post
- 대립가설 (H₁): μ_pre ≠ μ_post

서울대학교 교육통계 강의 자료. 사범대학교 교육학과 박현정교수
성태제(2019). 현대기초통계학 이해와 적용 제 8판. 학지사. pp, 255-268.
반응형
'교육연구방법' 카테고리의 다른 글
| 교육연구과 통계검증(10)- 회귀 (0) | 2025.04.11 |
|---|---|
| 교육연구과 통계검증(9)- 상관 (0) | 2025.04.11 |
| 교육연구과 통계검증(8)- t검증 (0) | 2025.04.09 |
| 교육연구와 통계방법(7) - 가설검증의 관점(불편파성, 구간추정, 표본크기) (0) | 2025.04.08 |
| 교육연구와 통계방법(5) -정규분포, 표집분포 (0) | 2025.04.07 |
| 교육연구와 통계방법(4) -분산도 (0) | 2025.04.06 |
| 교육연구와 통계방법(3) - 중심경향값 (0) | 2025.04.06 |
| 교육연구와 통계방법(2)- 그래프 (0) | 2025.04.03 |