◻ χ² 분포
▪ 분포의 형태: 자유도가 무한히 증가하면 좌우대칭의 정규분포가 되나, 일반적으로 정적 편포
▪ 자유도가 k인 χ² 분포는 모집단에서 k개의 z 점수를 표집하여 이들 z 점수를 제곱하여 합한 값들의 표집분포
▪ 따라서 자유도가 1인 χ² 분포는 z분포의 제곱과 동일
◻ 두 유목변수/범주변수간 독립성 검증
▪ 영가설: 한 변수의 분포는 나머지 다른 변수에 따라 다르지 않다 (변수간 독립성)
◽ 한 변수의 분포가 다른 변수에 따라 달라지는지
◻ 두 유목변수/범주변수간 독립성 검증의 기본 가정
▪ 관찰치의 독립성 가정 (observations, not variables, are independent of one another)
◽ 어떤 칸에 해당된 사례는 다른 칸에 해당된 사례와 상관이 없는 독립적 관계이어야
◻ 두 유목변수/범주변수간 독립성 검증
▪ Pearson's χ² test
▪ Fisher’s exact test
▪ Likelihood Ratio (LR) test

◻ Pearson’s χ² 검증과 Yates의 연속성에 대한 교정
▪ 2×2 이원분할표의 경우, Pearson의 χ² 검증은 유의확률을 과소추정함으로써 제1종의 오류가 커지는 경향
▪ 이 경우, Yates의 연속성에 대한 교정을 해주어야 함
◼ Yates의 연속성에 대한 교정:
▪ Pearson’s χ² 검증의 분자에서 제곱해주기 전에 0.5를 빼주고 계산
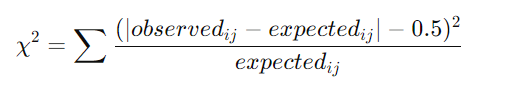
◻ Fisher’s exact test
▪ 일반적으로 2×2 이원분할표 혹은 표본크기가 작을 때 적용
▪ 행 합계 및 열 합계가 고정되어 있을 때, 이 때 가능한 모든 2×2 이원분할표를 구하고,
그 중 현재 관찰된 데이터보다 더 극단적인 결과가 나타날 확률을 계산
◼ 논란:
◽ 일방검증 혹은 양방검증?
◽ 현재 관찰된 데이터보다 “더 극단적인” 결과의 정의는?

■ 작은 기대빈도 (expected frequency)
- 표본 크기가 작은 경우, 얻을 수 있는 이원분류표의 수가 제한되어
관찰 데이터로부터 구한 χ² 검증통계량이 연속성을 가정하기 어려워지기 때문 - **특정 셀의 기대빈도(expected frequency)**가 5 미만일 경우에도 마찬가지 문제가 발생
(특히 기대빈도 5 미만 셀이 20% 이상일 경우) - 해결방안:
가능한 경우 주변 셀과 결합하여 기대빈도가 작은 셀을 없애거나,
Fisher’s Exact Test 혹은 Yates의 연속성에 대한 교정 시도
SPSS


3. 범주변수에 대한 효과크기 및 일치도
■ 범주변수에 대한 효과크기
- Odds
- Phi, Cramer's V
■ Odds (승산)
- 사고교육에 참여하지 않는 사례 대비 사고교육 참여 사례의 비율
- Odds Ratio (승산비; OR): 두 집단의 승산의 비율

■ 일치도
- 전체 사례 중 의견이 일치한 사례 비율
- 일치도 계산식:
일치도=(7+8+4+14)91=3391=0.363=36.3%\text{일치도} = \frac{(7 + 8 + 4 + 14)}{91} = \frac{33}{91} = 0.363 = 36.3\%일치도=91(7+8+4+14)=9133=0.363=36.3%



서울대학교 교육통계 강의 자료. 사범대학교 교육학과 박현정교수
성태제(2019). 현대기초통계학 이해와 적용 제 8판. 학지사. pp, 459-515.
'교육연구방법' 카테고리의 다른 글
| 교육연구과 통계검증(16)- 로지스틱 회귀분석 (0) | 2025.04.21 |
|---|---|
| 교육연구과 통계검증(14)- 공분산분석 (0) | 2025.04.16 |
| 교육연구과 통계검증(13)- 이원분산분석 (0) | 2025.04.16 |
| 교육연구과 통계검증(12)- 일원분산분석 (0) | 2025.04.15 |
| 교육연구과 통계검증(11)- 중다회귀분석 (1) | 2025.04.11 |
| 교육연구과 통계검증(10)- 회귀 (0) | 2025.04.11 |
| 교육연구과 통계검증(9)- 상관 (0) | 2025.04.11 |
| 교육연구과 통계검증(8)- t검증 (0) | 2025.04.09 |

