교육연구과 통계검증(13)- 이원분산분석

1. 이원분산분석의 기본 개념

■ 다원분산분석과 Factorial ANOVA

☑ 요인이 두 개 이상인 분산분석

☑ 다원분산분석은 요인의 수에 초점을 맞추어 제시된 표현

■ Factorial ANOVA

☑ 요인이 두 개 이상인 분산분석일 뿐 아니라, 각각의 요인을 다양한 구조를 설계할 수 있다는 점을 강조

☑ 요인의 수와 더불어 각 요인의 수준 수, 요인간 설계를 명확히 표현

☑ 예시:

학교 설립유형(국/공립, 사립)과 지역규모(대도시, 중소도시, 읍면지역)와의 두 요인을 함께 분석한 이원분산분석 ⇒ 2×3 요인설계

 

• 독립변수의 영향이 있는가와 두 독립변수의 상호작용이 존재하는가 : 교차 설계
• 한 독립변수의 각 수준에서 다른 독립변수의 영향이 있는지 : 내재설계

 

 

■ 이원분산분석 :

☑ 두 개의 독립변수 또는 두 개의 요인을 가지는 분산분석.

☑ 각 요인의 ‘주효과(main effect)’와 더불어 요인간 ‘상호작용 효과(interaction effect)’ 산출

☑ 일반적으로 요인간 상호작용 효과를 산출하고 검증하는데 연구자의 관심이 있을 때 사용

 

■ 주효과

• ☑ 요인 A의 주효과: 이원분할표에서 요인 A의 각 행 평균이 모집단에서 차이가 있는 것
• ☑ 요인 B의 주효과: 이원분할표에서 요인 B의 각 열 평균이 모집단에서 차이가 있는 것

 

■ 상호작용 (A×B) 효과

• ☑ 종속변수에 대한 요인 A의 효과가 요인 B의 각 수준에서 다르게 나타나는 것

 

 

■ 단순효과 (simple effects)

• ☑ 한 요인의 개별 수준에서 다른 요인의 효과
• ☑ 요인 A(설립구분)에서 요인 B(지역규모)의 단순효과:
  국공립학교 내에서 지역규모 효과와 사립학교 내에서 지역규모 효과
• ☑ 요인 B(지역규모)에서 요인 A(설립구분)의 단순효과:
  대도시 내에서 설립구분 효과와 중소도시 내에서 설립구분 효과, 읍면지역 내에서 설립구분 효과
• ☑ 상호작용효과가 유의할 경우 이를 좀 더 추가분석으로 시행 가능

 

 

교차설계 SPSS

이원분산교차설계.xlsx

0.01MB

 

 

 

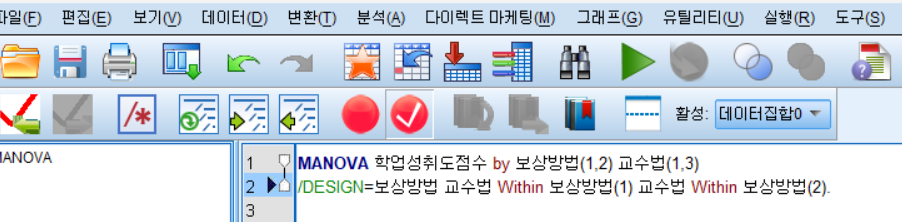
내재설계 SPSS

어떤 변수의 각 수준에서 다른 변수의 효과가 있는지 밝히는 설계.

 

 

 

 

 

서울대학교 교육통계 강의 자료. 사범대학교 교육학과 박현정교수

성태제(2019). 현대기초통계학 이해와 적용 제 8판. 학지사. pp, 421-458.